If you’ve been programming long enough, you’ve probably come across this oddity – operating on sorted arrays tends to be faster than unsorted. Why? The answer pertains to branch prediction. In this post, I will provide a brief overview of branch prediction as it pertains to programming (specifically Java). Examples are provided in terms of sorted and unsorted array processing, and a simple technique to “combat” branch prediction examined.
Branch Prediction
Branch prediction is a technique employed by processors to guess (predict) the path of a conditional statement prior to its execution to prefetch proceeding commands; theoretically providing a performance boost. In an environment dominated by true or false (assuming Boolean for the sake of simplicity) conditions, this approach achieves its intended effect. Take the following series of values and condition as an illustration:
Values \(v\): 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19
Condition \(c\): return (\(v<10\)) ? true : false;
The branch predictor quickly identifies a true pattern and predicts true correctly until 11. The predictor then realizes a guess of false is best, settling into that mode, correctly, for the remainder of the task. So what’s the problem?
The problem is, when the probability of branching is equal for each value, the branch predictor has a 50% chance of prefetching the wrong instructions, thus incurring an additional fetch cost to retrieve the correct commands. This results in an increased runtime. Take the following example:
Values \(v\): 0,10,1,11,2,12,3,13,4,14,5,15,6,16,7,17,8,18,9,19
Condition \(c\): return (\(v<10\)) ? true : false;
As you can see, the condition alternates between true and false over \(v\), resulting in an elevated runtime. A quick fix is to sort \(v\), allowing branch prediction to function as intended. However, the cost of sorting is generally \(O(n\log n)\), which can be prohibitively expensive for larger arrays.
Solution
The solution is quite simple (in premise) – avoid branching logic with 50/50 success/failure rates per value where possible. The question then becomes, how? The answer is a little less obvious and entirely dependent upon the conditions. Here, I will show you how to convert a simple one line if statement to convey the logic. Note: not all conditions can easily be replaced. This solution works well with numeric values.
BranchPrediction is a simple representation of the branch prediction problem. The task is as follows: given an array of \(n\) numbers, sum those greater-than-or-equal-to some condition. For testing, four approaches were implemented: process the unsorted array (lines 30-37), process an existing sorted array (lines 39-46), sort before processing (lines 48-62), and branch avoidance (lines 64-80). Let’s delve into branch avoidance.
import java.security.SecureRandom;
import java.util.Arrays;
/**
* Branch prediction example.
* @author Ray Hylock
*/
public class BranchPrediction {
private static int SIZE = 10000, MOD = 10000, CONDITION = MOD/2, ITERATIONS = 100000;
private static long SUM_B = 0, SUM_S = 0, SUM_R = 0, SUM_N = 0;
private static double TIME_B = 0d, TIME_S = 0d, TIME_R = 0d, TIME_N = 0d;
public static void main(String[] args) {
// Generate data
int v[] = new int[SIZE];
SecureRandom rnd = new SecureRandom();
for (int i=0; i<SIZE; i++) v[i] = rnd.nextInt()%MOD;
// sort generated data
int[] vS = new int[SIZE];
System.arraycopy(v, 0, vS, 0, v.length);
Arrays.sort(vS);
// run
branch(v);
sorted(vS);
sortRequired(v);
nonBranch(v);
output();
}
/** Branch prediction is inefficient. */
public static void branch(int[] v){
long start = System.nanoTime();
for(int j=0; j<ITERATIONS; j++)
for (int i=0; i<SIZE; i++)
if (v[i] >= CONDITION) SUM_B += v[i];
TIME_B += (System.nanoTime()-start)/1000000000.0;
}
/** Branch prediction is efficient. */
public static void sorted(int[] v){
long start = System.nanoTime();
for(int j=0; j<ITERATIONS; j++)
for (int i=0; i<SIZE; i++)
if (v[i] >= CONDITION) SUM_S += v[i];
TIME_S += (System.nanoTime()-start)/1000000000.0;
}
/** Branch prediction is efficient, but sorting overwhelms the runtime. */
public static void sortRequired(int[] v){
for(int j=0; j<ITERATIONS; j++){
// copy (not timed)
int[] vS = new int[v.length];
System.arraycopy(v, 0, vS, 0, v.length);
// sort (timed)
long start = System.nanoTime();
Arrays.sort(vS);
for (int i=0; i<SIZE; i++)
if (vS[i] >= CONDITION) SUM_R += vS[i];
TIME_R += (System.nanoTime()-start)/1000000000.0;
}
}
/** Avoid branching and is efficient. */
public static void nonBranch(int[] v){
long start = System.nanoTime();
for(int j=0; j<ITERATIONS; j++)
for(int i=0; i<SIZE; i++)
/* v[i]>=CONDITION can be rewritten as v[i]-CONDITION with bitwise
* operations to preserve the condition's intent. v[i]-CONDITION is
* right-shifted (>> instead of >>> as this hack relies on the sign
* bit) 31. As Java's numeric values implement two's complement,
* positive numbers lose their 1's and negatives 0's, resulting in 0
* (0...0) and -1 (1...1) respectively. Inverting the result
* (bitwise NOT) swaps the values. ANDing this with v[i] will
* produce either the v[i] or 0. Thus, it will add 0 or v[i] based
* on ~((v[i]-CONDITION)>>31). */
SUM_N += ~((v[i]-CONDITION) >> 31) & v[i];
TIME_N += (System.nanoTime()-start)/1000000000.0;
}
/** Outcome time and equality check. */
public static void output(){
// output time
System.out.println("Branch time: "+TIME_B+" seconds");
System.out.println("Sorted time: "+TIME_S+" seconds");
System.out.println("Sort required time: "+TIME_R+" seconds");
System.out.println("Non-branching time: "+TIME_N+" seconds");
// compare
boolean equiv = false;
if(SUM_B == SUM_S && SUM_S == SUM_R && SUM_R == SUM_N ) equiv = true;
System.out.println("Equivalence check: "+equiv);
}
}Branch Avoidance Example
So, how can we avoid using the if statement? Being an addition problem, we can use a 0/1 multiplier representing false and true respectively. That is, if the condition is false and the number is not to be added to the sum, the multiplier is 0, resulting in sum += (0)(v[i]) = sum. If the condition holds, then the multiplier is 1, resulting in sum += (1)(v[i]) = sum + v[i]. Great! Now how can we determine the multiplier with an if-style statement, which leads us straight back to the branch prediction problem? Good old-fashioned arithmetic and bitwise operations (line 78).
Taking v[i]-CONDITION results in either a positive or negative value (a binary solution like our 0/1 multiplier must be). Assuming an int for this example, if we shift (retaining the sign bit, so >> instead of >>>) 31 bits to the right, we are left with either 0 or -1. Zero represents a solution greater-than-or-equal-to the CONDITION, while -1, less-than. The bitwise NOT operator (~) swaps the values, so -1 is greater-than-or-equal-to and 0 is less-than. Why is this important? Because -1 is represented by all 1’s and 0 all 0’s. Thus, if we AND (&) with all 0’s we get 0 and will all 1’s, we get the original value. Thus, AND performs the multiplier action. Here are a few examples:
Let \(v[i]=8\) and \(c\) if(\(v[i]>=10\)) sum += v[i]8-10 = -2
-2 >> 31 = -1
~(-1) = 0
0 & 8 = 0
( 0000 0000
&0000 1000
---------
0000 0000 )
sum += 0 => sum
Let \(v[i]=22\) and \(c\) if(\(v[i]>=10\)) sum += v[i]22-10 = 12
12 >> 31 = 0
~(0) = -1
-1 & 22 = 22
( 1111 1111
&0001 0110
---------
0001 0110 )
sum += 22 => sum + 22
Experiments
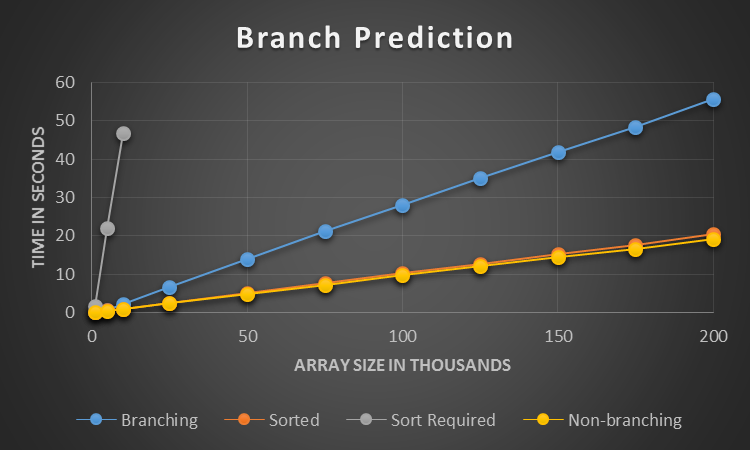
Lines 8-28 control the experiments. Static variables include the modulo (10,000), the condition (modulo/2), and the number of iterations (100,000). Modulo and condition are set to ensure the data are evenly distributed about the mean, resulting in 50/50 odds. The number of array elements (size) is dynamic. For these experiments, size (in thousands) is in the set {1, 5, 10, 25, 50, 75, 100, 125, 150, 17, 200} except for the sorting method, which was terminated after 10 due to execution time. Figure 1 represents the results.
Clearly, Sort Required is the poorest performer. Its time is dominated by sorting at each iteration. The distance between branching (unsorted array) and sorted/non-branching illustrates the impact of branch prediction failure. Sorted and non-branching are essentially the same (with a slight edge to non-branching), indicating the provided solution achieves the same level of efficiency as branch predication on sorted values. As most arrays are not pre-sorted, the clear choice is the non-branching approach – in this case.